Modelo dinámico de migración urbana e interurbana
12 de Septiembre de 2023

Edmundo Molina
Director de Investigación y Facultad

Hermilo Cortés
Investigador asociado
Introducción
¿Imaginas poder vivir cerca del lugar donde trabajas, estudias o te diviertes? ¿Cuántas personas podrían vivir ahí antes de que se saturaran los servicios o la vida se encareciera demasiado? En esta entrada al blog hacemos una demostración de cómo podemos aplicar la Ciencia de Decisiones, a través de la modelación matemática, para responder a estas preguntas.
El modelo describe la dinámica migratoria en un área urbana y sus alrededores. Como punto de partida tomamos en cuenta el modelo de Bracken & Tuckwell (1992) en donde la distancia al centro geográfico de una ciudad determina la densidad de población. De este trabajo, en particular, se toman en cuenta las distribuciones 𝜌(𝑟)=𝐴𝑒−𝑏𝑟 y 𝜌(𝑟)=𝐴𝑒−𝑏𝑟−𝑐𝑟2 con 𝐴,𝑏,𝑐 ∈𝑅, donde 𝜌 es la densidad de población y 𝑟 la distancia al centro, para generar una distribución de atractivo inmigrante, que es cuantificado por la probabilidad de inmigración (explicada más adelante). Las exponenciales con signo negativo generan una distribución tipo gaussiana alrededor del centro geográfico (𝑟=0).
En nuestro análisis, reinterpretamos el concepto de centro geográfico, generalizándolo a la idea de centro de atracción de un área o lugar de interés (económico o social) dentro de un área urbana determinada.
El modelo consiste en dividir el área urbana en celdas y en cada una de ellas determinar la densidad de población respecto a la vivienda. En cada paso temporal se hace crecer la población y la vivienda, implementando distintos modelos de crecimiento. Si la densidad de una celda rebasa cierta densidad límite 𝜌𝑙 entonces la celda en cuestión expulsa una fracción de la población. Dicha fracción puede ser fija o aleatoria en cada paso temporal.
La población expulsada en cada paso temporal de una celda se suma a la de las demás y se distribuye en toda el área de acuerdo a una probabilidad de inmigración, la cual varía en cada celda dependiendo de su distancia al centro de atracción y la cantidad de inmigrantes que llegó en el paso temporal anterior, haciendo esta probabilidad más grande si llegaron más inmigrantes. Esta es una idea similar, pero modificada, a la probabilidad de ocupación propuesta por Rybski & Kropp, (2013).
La combinación de estos elementos nos permite plantear hipótesis sobre las dinámicas por la que se guía el crecimiento de población y de vivienda, para proponer un modelo dinámico. En este modelo, en cada paso temporal se introduce un crecimiento poblacional y de vivienda. Para cada celda se calcula su densidad de población por vivienda, y, si esta densidad supera cierta cantidad, el sobrante de población (o una fracción fija o aleatoria de esta) es expulsada de la celda en cuestión. La población expulsada de todas las celdas es reubicada de acuerdo a la probabilidad de inmigración.
En los siguientes párrafos, explicamos cómo funciona el modelo y mostramos resultados de su dinámica bajo diferentes condiciones. Después de explicar a detalle las componentes del modelo, con el objeto de dotar a la discusión de un contexto realista, alimentamos el modelo con datos del área metropolitana del valle de México y sus alrededores, empleando el Censo de Población y Vivienda 2020, hecho por el INEGI.
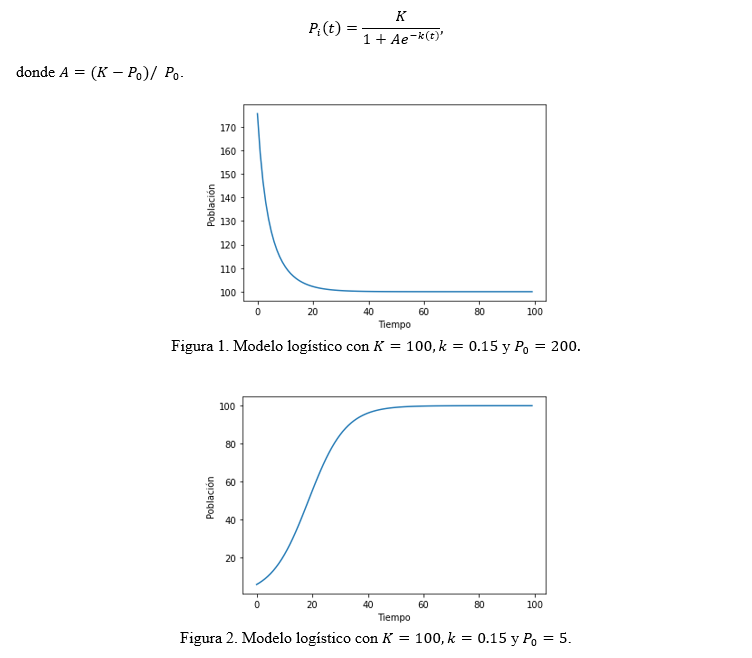
Crecimiento logístico con migración
En el modelo de migración la población inicial se actualiza en cada paso temporal, restando la población migrante y sumando la población inmigrante. En la Figura 3 se muestra un proceso logístico en el que en cada paso temporal la población inicial se le suma y resta una cantidad aleatoria, lo que se observa es que en un primer momento el comportamiento es aleatorio, pero después de ciertos pasos temporales el comportamiento logístico toma relevancia y la población se acerca asintóticamente a K.
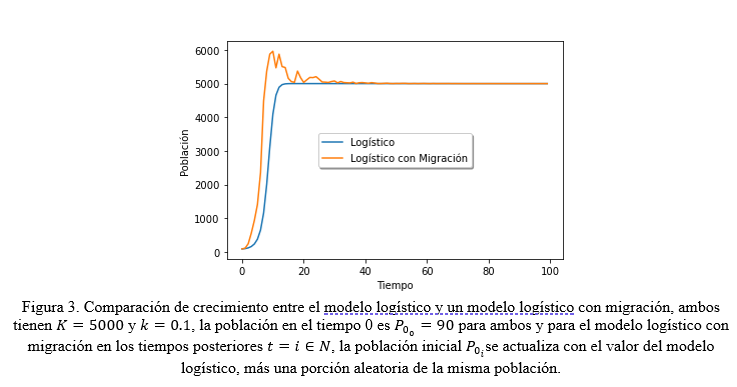
Para dotar de mayor flexibilidad a nuestro modelo, incluimos alternativamente un modelo mucho más simple, en el cual se aumenta en cada paso temporal una fracción de la población en el paso temporal anterior. Dicha fracción toma valores aleatorios dentro de una distribución normal entre 0 y 1 centrada en 0.5, es decir,
Crecimiento de vivienda
De manera similar al crecimiento de población, la cantidad de viviendas Vi(t) de la celda i crece en cada paso temporal. Este crecimiento es mucho más lento que el crecimiento de la población, bajo condiciones normales. En particular, consideramos tres diferentes patrones de crecimiento:
Crecimiento constante
Como punto de partida se toma el crecimiento de vivienda de la celda i ,V_i , constante en el tiempo, es decir
Es evidente que este crecimiento es más lento que el crecimiento logístico y proporcional de población.
Crecimiento proporcional
Una modificación a esta dinámica, es hacer crecer la vivienda de manera análoga al crecimiento poblacional, es decir,
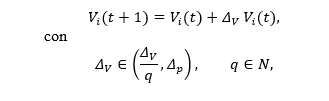
esto último para reflejar el hecho de que la vivienda crece más lento que la población, cuando la población crece de manera proporcional.
Si el crecimiento es logístico, al tener un crecimiento sigmoideo (de la función sigmoide o logística, como en la Figura 3) en los primeros momentos, y dado que V_i (0)<P_i (0), siempre que Δ_V<0.5 la dinámica de crecimiento de la población será mayor que la de vivienda en los primeros momentos. Como el modelo logístico tiende a estabilizarse, después de un tiempo la vivienda tiende a superar a la población, por lo que esta combinación de crecimientos no es muy realista para tiempos largos.
Crecimiento logístico
Otra posibilidad es utilizar el mapeo logístico en un régimen en el que se estabiliza “desde abajo'', es decir, que tiende al valor de la capacidad de carga K_V, aproximándose por valores inferiores a este (Figura 2). Esto puede reflejar el hecho de que la vivienda puede crecer hasta cierto punto y más adelante permanece constante. Para que este crecimiento sea más lento que el de población hay que tomar una tasa de crecimiento suficientemente pequeña y una capacidad de carga menor.
Modelo de migración
El modelo de migración integra las dinámicas de crecimiento de población y de vivienda explicadas en las secciones anteriores. Para cada celda, se calcula su densidad de población por vivienda, y, si esta densidad supera cierta cantidad, el sobrante de población (o una fracción fija o aleatoria de esta) es expulsada de la celda en cuestión. La población expulsada de todas las celdas es reubicada de acuerdo a la probabilidad de inmigración. Esta dinámica se repite en cada paso temporal.
Para cada celda i, se calcula su densidad de población por vivienda como
En cada intervalo de tiempo si las condiciones de esa celda inhiben o incentivan la migración. Si la densidad supera un límite ρ_l definido, entonces se suscita un patrón de expulsión. Cuando en la celda i se cumple este criterio en el tiempo t^*, es decir, ρ_i (t^*)> ρ_l , de esta celda se sustrae una porción de la población excedente P_(exc_i ) (t^*), la cual se calcula de la siguiente manera

La porción Δ_e∈(0,1) que se sustrae puede ser fija en el tiempo o puede ser aleatoria, escogida de una distribución uniforme en el intervalo (Δ_emin,Δ_emax)⊂(0,1). La elección de Δ_e fija en el tiempo lleva a un modelo determinista cuando la población y la vivienda crecen de manera no aleatoria (modelo logístico en ambas o logístico en población y vivienda constante).
La población expulsada en cada paso temporal de cada celda se suma a la de las demás celdas y se distribuye en toda el área de acuerdo a una probabilidad de inmigración, P_(Inm_i ) (t), la cual varía en cada celda, dependiendo de su distancia r_i al centro de atracción y la proporción de inmigrantes nuevos respecto a la población total que llegó en el paso temporal anterior P_(I_i ) (t), haciendo esta probabilidad más grande si llegaron más inmigrantes:
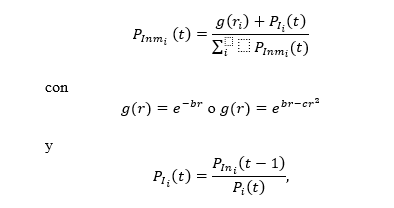
donde 〖P_In〗_i (t) es la población inmigrante de la celda i al tiempo t. La probabilidad de inmigración se divide por la suma de su valor en toda la malla, con la finalidad de que al sumar la probabilidad de todas las celdas sume 1, así se asegura que se reparta correctamente la población expulsada (sin excesos, ni decesos).
Resultados con datos reales
En esta sección se muestran resultados de simulaciones realizadas con los de datos del censo de población y vivienda 2020 realizado por el INEGI, en particular analizamos la zona metropolitana del valle de México.
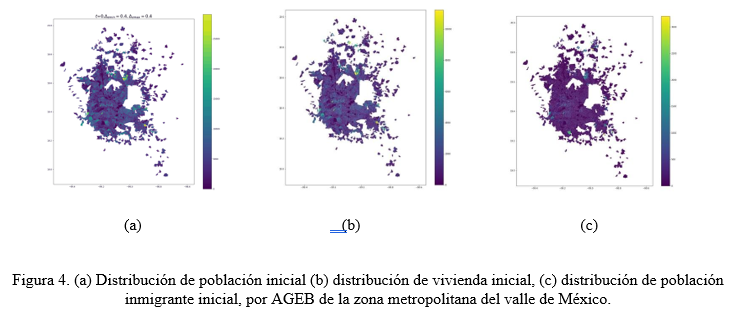
Las celdas de la malla de las simulaciones son las áreas geoestadísticas básicas (AGEB) en las que el INEGI divide el área territorial Mexicana para hacer el censo. Como datos iniciales se tomó la población de las AGEBs del área en cuestión como la distribución de población inicial (Figura 4 (a)). El censo también tiene datos de la cantidad de viviendas por AGEB con lo que se tiene la distribución inicial de vivienda (Figura 4 (b)). La distribución de población inmigrante inicial se tomó como la cantidad de personas que en el censo contestaron que no vivían en esa ciudad en 2015 (Figura 4 (c)).
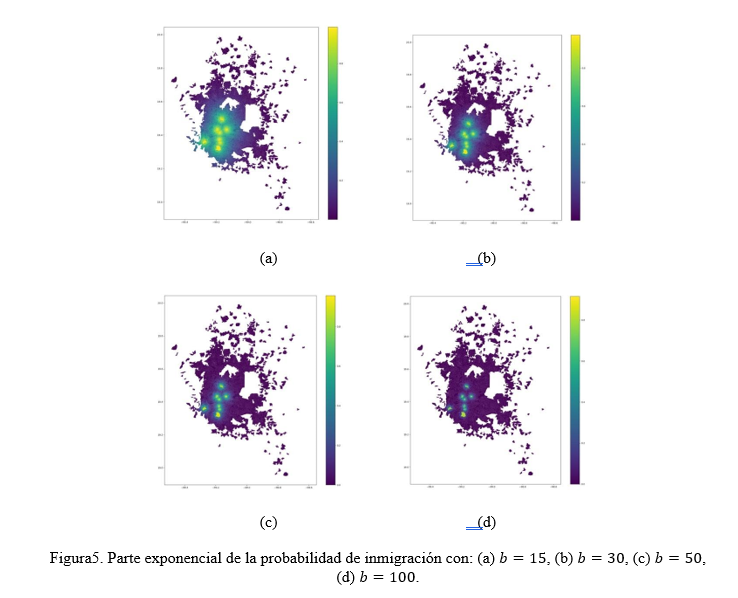
La probabilidad de inmigración inicial se determinó ubicando los principales centros laborales a través de la Encuesta Origen Destino en Hogares de la Zona Metropolitana del Valle de México (EOD) 2017, es decir: Zócalo, Condesa, Reforma, Col. del Valle, Metro viveros, Zona industrial Vallejo, Ciudad Universitaria, Polanco y Santa Fe. Se calculó la distancia geodésica de los centroides de cada AGEB i a estos centros y para cada uno se tomó la distancia más corta como la distancia r_i para la que se calcula la parte exponencial de la probabilidad de inmigración e^(-br_i ) (Figura 5). Por esta elección de centros de atracción, la simulación se puede interpretar como la distribución de población que surgiría si la gente migrara cerca de su lugar de trabajo. Estos resultados no representan una dinámica realista, pero principalmente ilustran los mecanismos de interacción del modelo.
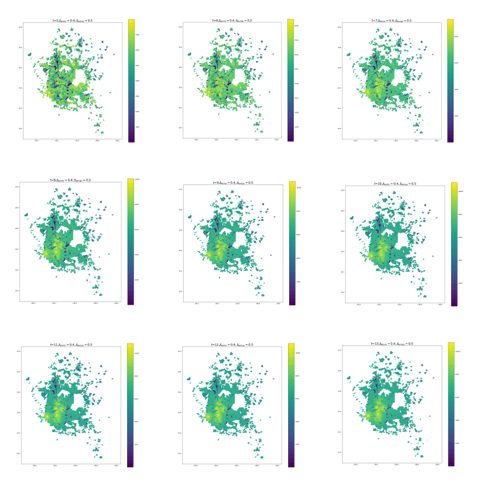
En este análisis de simulación, el modelo de crecimiento de población con el que se trabajó fue el logístico con parámetros: máximo de población por celda, K_p=6500, y parámetro de crecimiento logístico, k_p=0.1. La dinámica de crecimiento de vivienda se captura a través de un modelo logístico con parámetros: máximo de viviendaK_v=1000 y parámetro de crecimiento logístico k_v=0.01. La densidad límite del criterio de expulsión de población fue ρ_l=6 y la porción expulsados se explora sobre una distribución uniforme (Δ_emin,Δ_emax)⊂(0,1), en donde Δ_emin=0.4,〖 Δ〗_(emax )=0.5. El parámetro de atracción exponencial de la probabilidad de inmigración fue tomado como b=30. La dinámica de migración resultante de esta simulación se muestra en la Figura 6.
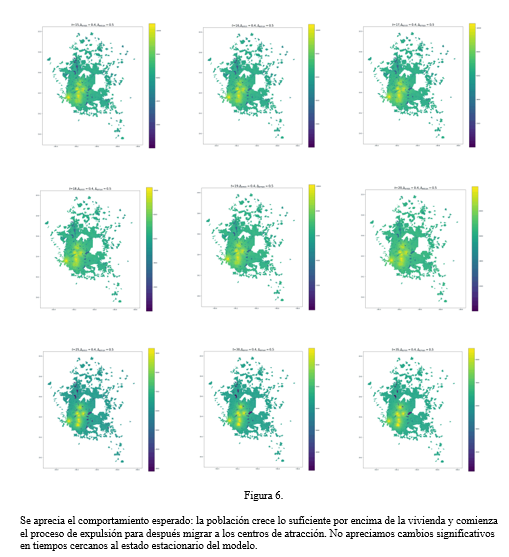
Sobre la variación de parámetros, particularmente respecto a el parámetro de atracción exponencial de la probabilidad de inmigración , b, y la fracción de expulsados en cada paso temporal, Δ_e, se pueden concluir dos cosas: La primera es que a mayor b en la parte exponencial, mayor es la concentración en los centros. Esto se puede explicar de manera sencilla, ya que la exponencial e^(-br) decae más rápido respecto a r cuando b es más grande. Entonces, para b mayor se genera una diferencia mas grande en la probabilidad de inmigración entre zonas cercanas y lejanas a los centros, como se puede apreciar en la figura 5. La segunda es que al incrementar el intervalo de aleatoriedad de la fracción de expulsados, (Δ_emin,Δ_emax), la diferencia de concentración en las AGEBs cercanas a los centros respecto a las AGEBs lejanas es menos marcada.
Conclusiones
El modelo presentado en este trabajo muestra tendencias que pueden ser de utilidad para explicar fenómenos de migración en áreas urbanas. Las distintas combinaciones de dinámicas de crecimiento de población y vivienda, así como las posibilidades para escoger los parámetros en el modelo de migración permiten adaptar el modelo a distintas situaciones de ciudades y áreas urbanas de México y del mundo. Al poder variar entre lo determinista y lo aleatorio (variando el intervalo(Δ_emin,Δ_emax)) el modelo exhibe comportamientos como los observados en otros sistemas complejos y por ende tiene posibilidades de simular o aproximarse a aspectos de dichos sistemas. La posibilidad de elegir qué tanto atraen los centros (variando b) y que tan marcada es la diferencia de población concentrada en estos respecto a otros lugares (variando Δ_e), dan al modelo bastante dinamismo y se puede aprovechar para modelar situaciones reales con mayor detalle. Más datos de tipo económico, social, geográfico, cultural, podrían ser empleados para modelar de forma multi-dimensional el tipo de atracción en cada lugar y tener un modelo dinámico con mayor granularidad.
Trabajo futuro
Entender de manera más precisa y cuantitativa el modelo de migración. Para ello se pueden utilizar métodos de clasificación, como agrupación jerárquica (hierarchical clustering), k-vecinos más próximos u otras para entender las similitudes y diferencias entre AGEBs. Con el mismo fin, se podrían utilizar métricas provenientes de teoría de redes, para determinar las celdas o AGEBs que están conectados basándose en sus propiedades de población, vivienda, densidad, o incluir aspectos sociales económicos o culturales que las relacionen.
Desarrollar un criterio de migración preferencial diferenciada en el que el atractivo migrante varíe de un estrato social a otro, tomando en cuenta aspectos laborales, económicos, sociales, culturales u otros. Esto se podría lograr haciendo matrices de probabilidad de inmigración diferenciadas para cada sector de la población.
Tomar en cuenta aspectos geográficos, geopolíticos, económicos y/o sociales de las áreas urbanas con las que se trabaja, ya sea para poner límites al crecimiento de vivienda, o barreras de crecimiento de población en las áreas que corresponda, o lo contrario, acelerar el crecimiento de vivienda en zonas donde haya un auge de inversión por alguna razón, o que haya zonas donde la población puede y tiende a ir. Esta información podría modificar los parámetros locales de los modelos de crecimiento tanto de población como de vivienda, de manera diferenciada.
Bracken, A. J., & Tuckwell, H. C. (1992). Simple mathematical models for urban growth. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 438(1902), 171-181.
Rybski, D., Ros, A. G. C., & Kropp, J. P. (2013). Distance-weighted city growth. Physical Review E, 87(4), 042114.
Strogatz, S. H. (2018). Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering. CRC press.